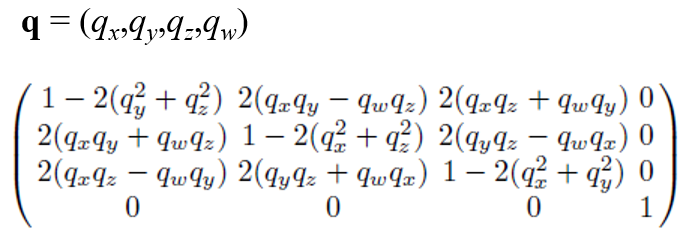Quaternion (사원수)

3D의 Transform 속성에는 네 가지가 있다.

  • Position
  • Rotation
  • Scale
  • Quaternion

이중 세가지는 상식적으로 이해할 수 있는데 Quaternion은 생소한 경우가 많다. 회전에는 Euler(오일러)와 Quaternion(쿼터니언)이 있는데 Euler가 일반적인 Rotation이고 이것을 보완해 나온 것이 Quaternion이다.

Euler는 X, Y, Z 축에 대한 회전을 표현하는 것이다. 하지만 단순히 각 축에 대하여 각도를 지정하는 것만으로는 회전이 고유하게 정해지지 않고 축에대한 회전의 순서에 따라 다르게 나타나기도 한다. Euler로 표현하는 것의 한계는 짐벌락현상과 보간을 예로 들 수 있다.

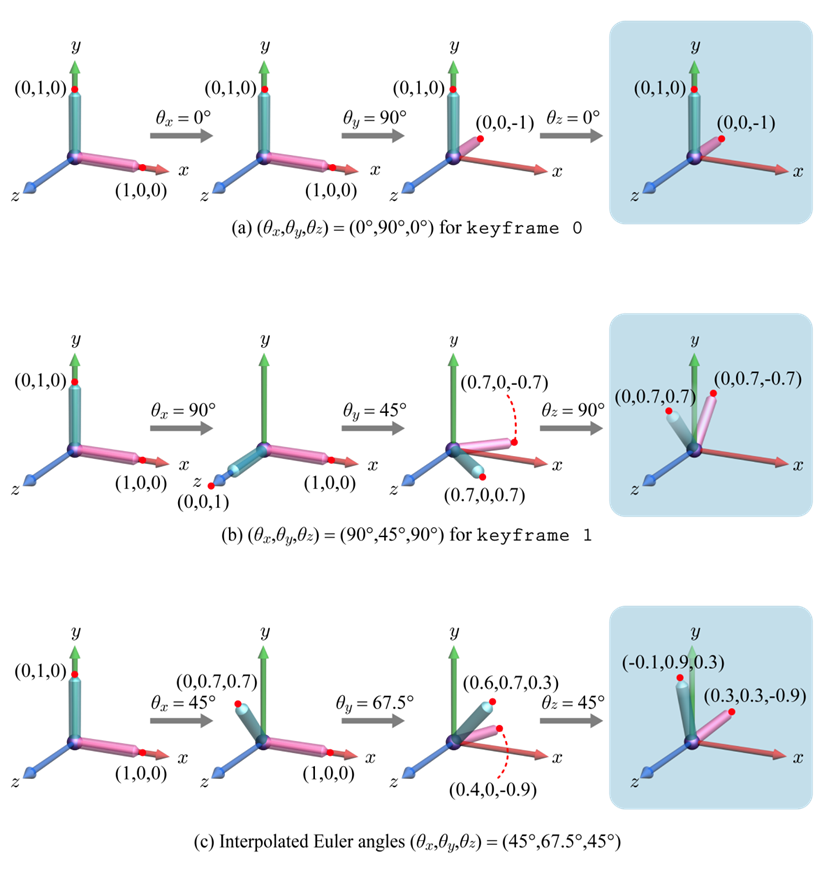
result

보간의 경우 위 그림에서 첫 번째와 두 번째 줄의 회전 변환 결과 사이를 보간한다고 가정했을 때, 첫 번째와 두 번째 줄의 회전 변환의 결과는 모두 yz-plane 평면상에 있으므로 보간한 결과들 역시 yz-plane 평면상에 있어야 할거 같다. 하지만 세 번째 줄의 결과를 보면 그렇지 않다. 이렇듯 Euler Angle를 사용하면 문제가 생길 수 있는 것이다.

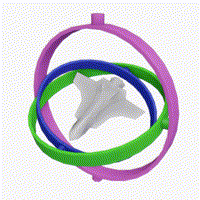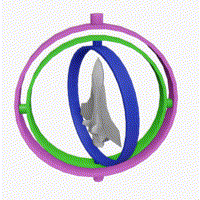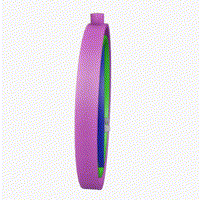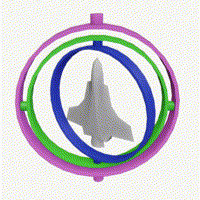
result

짐벌락 현상의 경우 간단히 요약하자면, X, Y, Z축으로의 회전을 일정 순서로 진행하게 되면 두 축이 겹친 경우 다른 두 축의 회전이 동일해지기 때문에 한 축의 기능을 상실하게 된다는 내용이다.

Quaternion이란 4차원 벡터를 뜻하는 말로 4원수하고도 한다. 복소수를 이용해 이러한 문제를 해결했다는 선에서 이해하고 넘어갔다. KUOCW 한정현 교수님 강의 자료를 첨부하겠다.

KUOCW 한정현 교수님 강의 자료

Quaternion의 정의와 성질

하지만 Quaternion은 위의 문제를 해결할 수 있습니다. Quaternion이란 4차원 벡터를 뜻하는 말입니다. 한국말로는 4원수라고도 하죠. 여기서 복소수의 개념이 등장합니다. 아래와 같이 Quaternion을 정의하죠 왼쪽부터 3가지 항은 각각 다른 허수 축을 가지는 허수부로 오른쪽은 실수부를 나타냅니다. 세 가지 허수부를 줄여서 _v로 나타내기도 하죠.

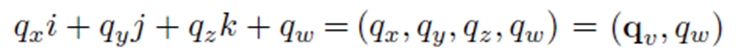result Quaternion

그리고 기본적인 두 Quaternion의 연산과 각 축에 대한 성질 은은 아래와 같습니다.

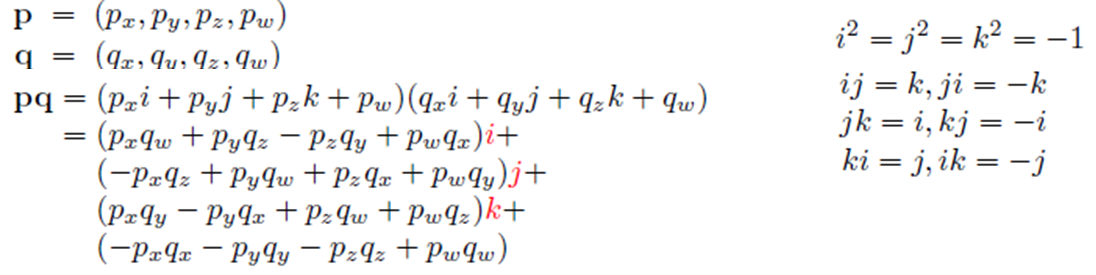result Quaternion 연산

또한 Quaternion의 켤례 복소수와 크기는 아래와 같이 표현되죠.

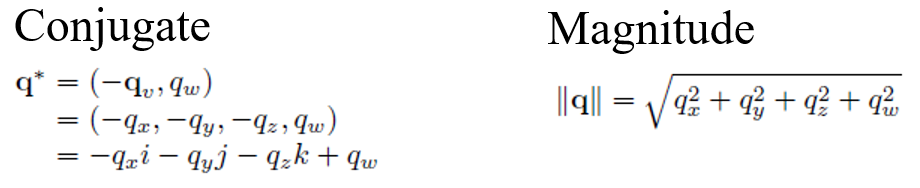result Quaternion의 켤례 복소수와 크기

Quaternion을 이용한 회전

우선 복소수를 이용해 2D회전에 먼저 적용시켜 보겠습니다. 아래 그림과 같이 점 p(x, y)에서 점 p'(x', y')로 θ만큼 회전을 한다고 합시다. 이때 p를 복소수를 이용하여 x+yi로 나타내고 또 θ를 이용해 cosθ+sinθi로 하고 pq를 연산하면 실수부는 x'을 나타내고 허수부는 y'을 타나 내는 것을 확인할 수 있죠. 신기하게도 복소수를 이용해 회전에 관련된 값을 계산할 수 있는 것입니다. 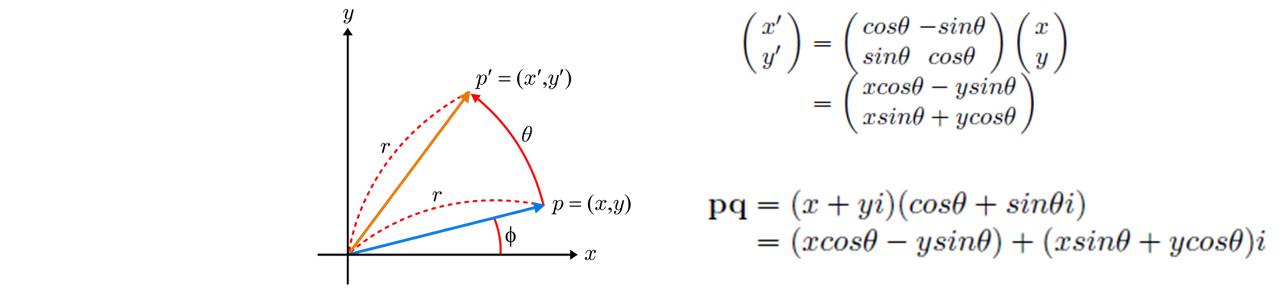result 복소수를 이용한 회전변환의 표현

그렇다면 3D에서는 어떻게 표현될까요? 3D에서는 한 가지 허수 축이 아니라 3가지 허수 축이 있는 Quaternion을 사용합니다. 아래와 같이 u라는 축을 기준으로 θ만큼 p에서 p'으로 회전을 한다고 가정해 봅시다. 그리고 p점의 x, y, z 좌표는 Quaternion의 허수부 p_x, p_y, p_z에 들어가고, 회전을 나타내는 Quaternion은 θ와 회전축 방향으로의 단위 벡터 u를 이용해 아래와 같이 q로 표현이 됩니다. 이때 위의 2D rotation을 복소수로 나타내면 그 값들을 찾을 수 있는 거 같이 3D에서는 이 Quaternion을 이용하여 qpq*연산을 하면 그 허수부가 회전한 x', y', z'을 나타낸다고 합니다(증명 생략). 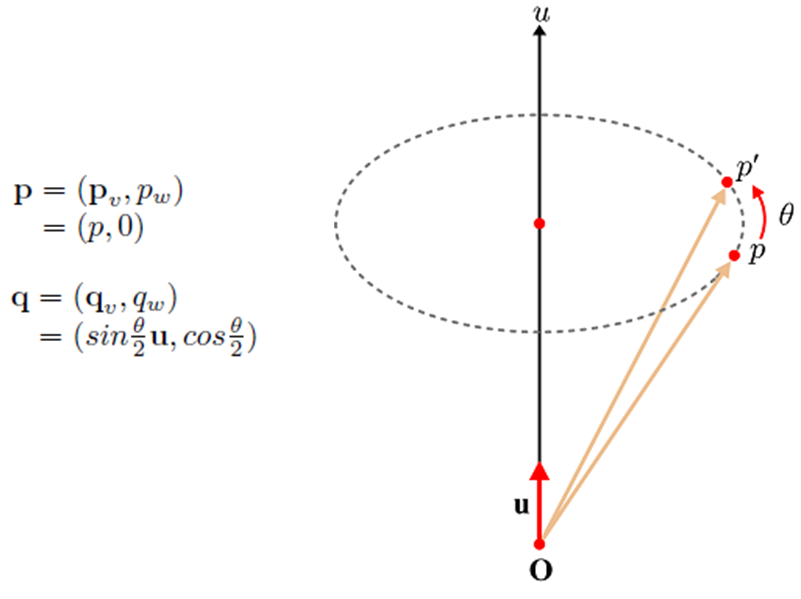result Quaternion을 이용한 회전

이렇게 Quaternion을 이용하여 회전할 수 있게 되면, 굳이 문제가 생길 수 있는 Euler Angle을 이용하는 것이 아니라 임의의 축을 기준으로 회전시키면 되는 것이죠. 또한 앞서 문제가 되었던 회전 변환에 대한 보간도 Quaternion은 해결할 수 있습니다.

아래 그림과 같이 xyz 좌표를 아는 unit quaternion p 그리고 q를 가정했을 때, 그림 옆의 수식같이 보간이 가능합니다. 이때 ∅값은 두 quaternion의 내적을 통해 구할 수 있습니다. Unit quaternion이기 때문에 ||p||=||q||=1이 되고 따라서 ||p||*||q||*cos∅ = cos∅로 나타낼 수 있죠. 이때 각 좌표 성분 간의 곱을 합한 게 내적의 값이기도 하기 때문에 arccos을 통해 ∅를 충분히 구할 수 있죠. 따라서 아래 수식을 풀 수 있고, 보간이 가능한 것입니다. 이를 spherical linear interpolation (slerp)라고 부릅니다. 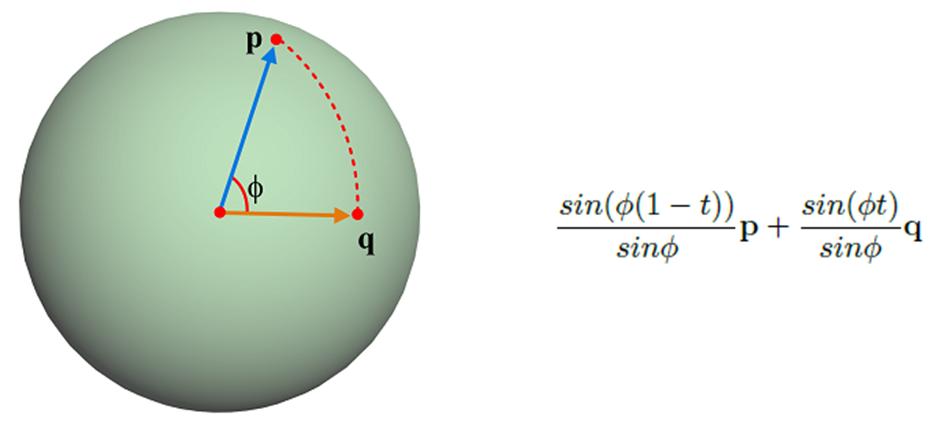result spherical linear interpolation(slerp)

마지막으로 Quaternion 역시 Euler angle과 같이 4x4 matrix에 들어가서 표현될 수 있습니다. 아래는 Quaternion을 통한 rotation matrix를 표현한 것입니다. 이때 q는 (sin(θ/2)u, cos(θ/2))일 거 같습니다. 증명은 강의에서도 다루지 않아 저도 넘어가겠습니다. 이로써 Euler angle의 역할을 Quaternion이 다 해낼 수 있는 것이죠. result